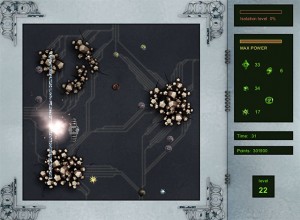
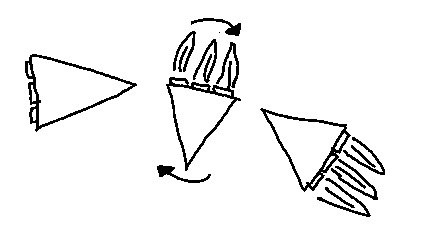Games

♥ Princesses versus giraffes ♥

TLDR; I’m writing a coop multiplayer game with my daughter, this is the current result! Works in Firefox and Chrome. Use arrows to move and space to fire. Share a URL to play with a friend.

Some years ago, my daughter figured out I made some computer games, and she even played one of them quite a bit. After a while she wanted something new, and we figured we’ll make a game together. She would draw concepts and come up with ideas, and I would try to make them happen in game.

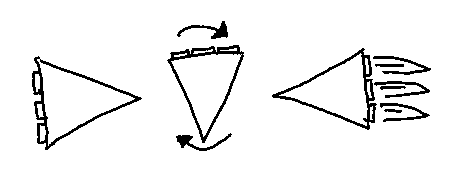
The initial concepts she drew were these:

We then together made them into vector with some modifications.

Princess and "giraffe" — A princess and a giraffe… I guess

Tips on kid friendly vector drawing programs would be very much appreciated, throw me an email or post a comment. We used Sketch, but Sketch is a bit overwhelming and distracting with all its features. I want a program which only have bezier patches and transformations on them, as well as fill, stroke and possibly opacity settings.

Going from concepts to a prototype

I had been wanting to try compile to JS with Kotlin for a while, so I started a project in IntelliJ and quickly threw something together using a plain HTLM5 Canvas.

We drew some more concepts, and after some evenings implementing we had an infinite randomly generated castle, an arrow firing princess, a hyperactive bow carrying giraffe, and a bunch of collision detection bugs (yay for rolling your own).

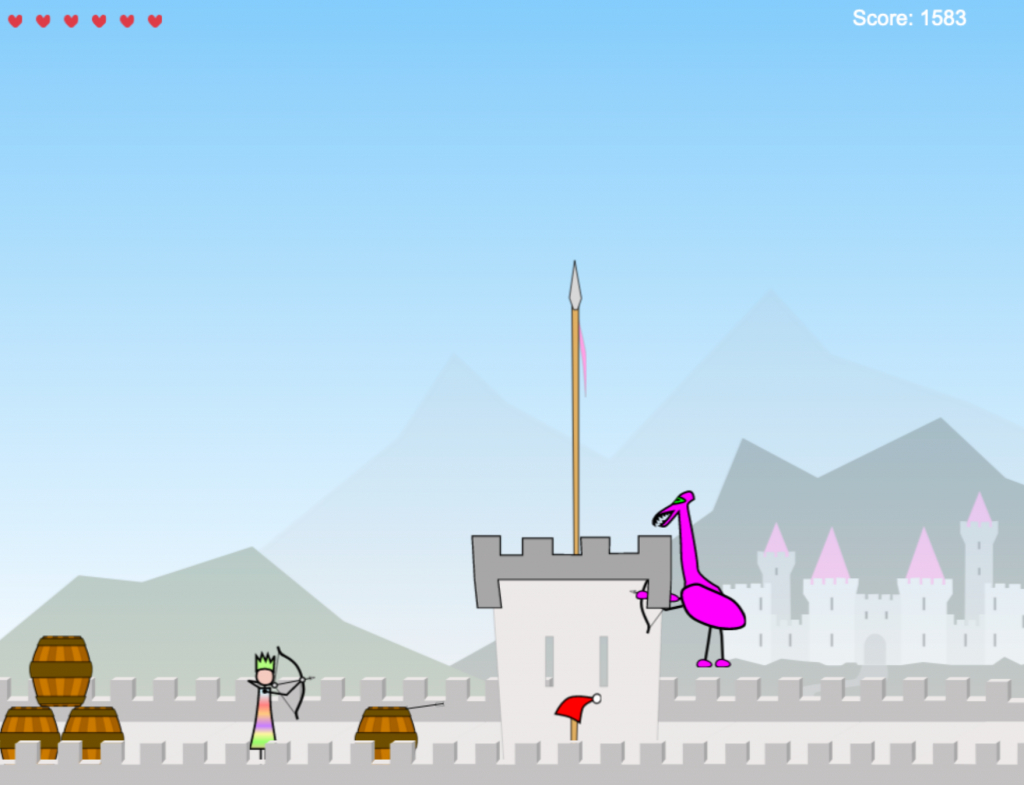
Wriggling out of hard requirements

After a lot of fun triggering bugs, my daughter came up with some new requirements.

I want to play with my friends, and we should all be princesses!

These are sort of hard to implement, disregarding networking, it would mean a total rewrite of how the world generation and camera worked. It would also need a solution for how to avoid someone getting stuck due to the camera movement of others and so on.

Those giraffes are in for a surprise.

After some bargaining we made some new concepts, and we agreed to add a player controlled cloud, and a bunch of new giraffes.

Adding networking

For me this meant that I would need to add some kind of networking to the game. For browser games, the choices are:

Communicate with a server using WebSocket and have that relay state, or run the game on the server.
Negotiate a WebRTC datachannel, and send communication directly between the browsers.
Have players install a browser extension like netcode.io,and use it instead of WebSocket.

Since the game is cooperative, there is little reason to run the game on a server. Actually I really, really do not want to run the game on server, for a bunch of reasons, mostly for abuse and scaling troubles.

Using a server as a relay of state or input is also a bit funky, since it will introduce a lot of unnecessary latency. Since I am also willing to sacrifice some poor kids behind a symmetric NAT, I decided for option 2 and I have not regretted that.

I was cautious about doing this initially, since I had read this Gaffer on Games post which deemed WebRTC too complex, though that was in the context of server based architectures.

Having some more experience with WebRTC now, I agree a bit about the complexity, though I think it has gotten way better, especially with a more stable standard and more complete alternative implementations like rawrtc. I also ♥ how WebRTC abstracts away most of the P2P complications behind a very nice API.

Autorative peer or GGPO?

To share state in the game, I needed to come up with an architecture for networking. Initially I evaluated using something like GGPO, but in the end I chose to go with using the princess peer as an autorative peer, and sync the state to the cloud playing peer continuously, while the cloud peer only sends input. I chose this mostly for simplicity and time constraints. Since the game is cooperative, a lack of fairness is also not really a problem.

For the amount of work i put in, I am very pleased with how the networking worked out. Right now it is not tuned at all, just JSON over the datachannel, but even without tuning and no extra speculative integration, it has worked fairly well.

Where to go from here.

While the game is in a state of continuous updates, I think it is mostly just going to be small changes from now on. Maybe some sound effects and new graphics when we feel like it.

Rendering is currently also quite slow, and takes a lot of the frame budget. I would like to migrate to a framework with a WebGL based renderer. But sadly that seems like quite a bit of work, mostly due to using SVGs for graphics.

For future projects game projects, I will for sure start with a WebGL based framework, or possibly Unity tiny, and raster based images.

That is all for now, go and see how far you can get in our game!

One way to stop a 2D spaceship as fast as possible.

For a quite a while, I have wanted to try and create simple touch based interface for a 2D spaceship game. I want to allow the player to simply drag anywhere on the screen, and the spaceship moves to that position and direction in an efficient manner. Ideally the most efficient manner.

Spaceships in 2D games usually have one main engine that allows forward thrust, and some that allow rotation around the ships center of mass.

Moving from point A to B efficiently (in minimal time) is not trivial with such constraints, as changes to direction and thrust may have huge consequences for later possible movements due to inertia.

So instead of looking at the full A to B problem immediately, I wanted to look at something simpler first, namely to go from having velocity $v_0$ and pointing in direction $\theta_0$ to have 0 velocity as fast as possible.

The idea I use originally came from talking to a colleague, but something very similar sounding is mentioned in planning algorithms, though examples always seems to involve driftless systems. Anyway, my current approach involves these known quantities and assumptions:

$a$ – Acceleration – The ship can only accelerate by a constant amount, and acceleration turns on and off instantly.
$s$ – Turn speed – rotating the ship requires no acceleration, and the ship has constant rotation rate.
$\theta_0$ – Initial orientation.
$v_0$ – Initial velocity

These quantities allow me to find a legal, but very suboptimal way to stop. It simply involves to turn the ship to face its velocity vector, and then accelerate until it stops. Both the time needed to turn the ship $t_a$ and the time $t_m$ needed to turn and reverse the velocity are easy to calculate.

Turn until facing velocity and initiate burn at time $t_a$. At $t_m$ the ship has velocity 0.

It is also easy to see that this is suboptimal, it would clearly be faster, to start burning some time before the turn is fully completed, but the question is when to start the burn.

To allow for this freedom in my model, I therefore introduce a third time variable $t_s$. $t_s$ is the time to start turning and accelerating at the same time. $t_a$ now becomes the time when I stop turning and only accelerate.

Turn and initiate burn after $t_s$ time, at $t_a$ time only accelerate. At $t_m$ the ship has velocity 0.

Given these intervals, two integrals describe how the velocity will change when $t_s$, $t_a$ and $t_m$ vary.

$$ v_x = \int_{t_s}^{t_a} a\cos(\theta_0+st)dt + \int_{t_a}^{t_m} a\cos(\theta_0+st_a)dt $$

$$ v_y = \int_{t_s}^{t_a} a\sin(\theta_0+st)dt + \int_{t_a}^{t_m} a\sin(\theta_0+st_a)dt $$

This gives two constraints, that must hold for all solutions of this kind.

$$ 0 = v_{0x} + \int_{t_s}^{t_a} a\cos(\theta_0+st)dt + \int_{t_a}^{t_m} a\cos(\theta_0+st_a)dt $$

$$ 0 = v_{0y} + \int_{t_s}^{t_a} a\sin(\theta_0+st)dt + \int_{t_a}^{t_m} a\sin(\theta_0+st_a)dt $$

The most efficient solution to this problem, is the $t_s$, $t_a$ and $t_m$ triplet with the lowest value for $t_m$.

This information allows me to formulate this as a optimization problem.

Since I want to minimise $t_m$, the objective function simply becomes ${t_m}^2$.

This is subject to the two equality constraints given.

Since the objective and constraints are non-linear, I plug i into Optizelle which is a framework for solving non-linear optimization problems.

The implementation can be found on github, it uses autograd, to calculate derivatives and hessians. This is an incredible time saver since calculating 9 combinations of partial derivatives would have been a major pain, not to mention having to recalculate them whenever I did something wrong.

Running the program with inputs $a=2.0$, $\theta_0=0$, $v_0=[2,0]$ and $s=\frac{\pi}{2}$ returns:

The optimal point vector contains the values for $t_s$,$t_a$ and $t_m$. This means that for a ship with the given input, it should start turning immediately, then start the burn after approximately 1.43 seconds, stop turning and only accelerate at 2.43 and finally be at rest after 2.57 seconds, approximately 0.43 seconds faster then the naive version.

To test the result, I implemented a quick and dirty javascript program that simulates these choices and renders to a canvas:

Sometimes the ships end up drifting a bit after the simulation has finished. This is due to the discrete nature of the simulation not perfectly emulating the continuous solution (I do not integrate rotation analytically in the simulation). This could also have been a problem if I applied this style of planning to a game that did the same, from the simulation above it looks negligible though, which is great!

I am very happy with this result, it seems like it could work for the larger problem as well. The next step I’ll try, is to tackle some specific cases of moving from point A to B efficiently. For those cases there will be many more time variables involved, and possibly many constellations of safe initial starting points as well as possible freedoms to introduce in the model. It will be interesting to see how that works out.

Solving Get1000 continued…

In one of my previous posts, I laid out a plan to solve the Get 1000 game. It turns out that plan was wrong.

My expectiminimax based solution works well for a game with random elements and perfect information, but it is not very useful for a game with imperfect information. Get1000 is played simultaneously by the players, and the opponents choices are hidden until the end of the game.

This meant I had to go back to find a new strategy for solving the game. I decided to try and find the correct brute force way first, and then see if that could be made faster in some way.

Exploring brute force

A solution to the game involves finding a Nash equilibrium from all the pure strategies of the game. A brute force solution could be done by creating a matrix where all pure strategies are pitted against all the other pure strategies.

The full payoff matrix needed for a normal form brute force solution.

A strategy here refers to a function $S \rightarrow Pl$ which given any game state $S$ gives a Get1000 placement $Pl$ . Below is an illustration of what i mean by a state. A state could also include the history (order of placement), which would increase the count a lot, but that is hopefully not needed for a solution.

A gamestate can be represented as the current number (in this case 1), the entries in hundres (7), tens (5) and ones (12) as well as the amount of free positions for hundreds (1), tens (2), ones(2).

The total amount of such states is $211248$ but in at least $27648\cdot3$ the choice is forced. This means there are at most. $211248 - 27648\cdot3 = 128304$ relevant states, probably quite a bit fewer.

Each state has at most 3 choices, therefore there is an upper bound of $M = 3^{128304}$ unique pure strategies.

This is of course not that helpful, since a $3^{128304}\times3^{128304}$ matrix is enormous, and for each cell in the matrix all possible $6^9$ games would have to be played to find the payoff $P$ for the pure strategy pairs. On top of that, the best mixed strategy would then have to be calculated.

Subgame perfection and backwards induction

Modeling this in normal form as above seemed to get me nowhere, I therefore turned to extensive form, and something called subgame-perfect nash equilibria, and backwards induction. In the normal form solution I need to look at all possible strategies. Using subgame perfection, I hoped to get away with only looking at a very small subset.

While this sounds straighforward in theory, I found it quite hard to figure out where my information sets are, and whether I could consider each choice node in Get1000 a subgame. After struggling for a while, I ended up with an extensive form structure looking like this. Players are P1 and P2, and “move by nature” is the dice roll.

Extensive form of a game with the same structure as Get1000. As players do their choices, the information sets get larger and larger. Since the “moves by nature” are known by all, they do not increase the information sets.

This structure means that only the roots of the tree are subgames, since all other nodes are part of larger information sets.

Attempting backwards induction

The above structure means that it is not practical to naively use subgame perfection and backwards induction to solve the game, but taking inspiration from it could still be useful to get a good strategy.

The algorithm for subgame perfection goes like this:

Consider the final subgames (those with no further subgames), pick a Nash equilibrium as solution there.
When considering the next subgames up the tree, the payoffs in the subgames already considered are used to create the payoff matrix.
Iterate step 2 until the root node of the extensive form tree is reached.

To get something working, I pretend that the other player is at the same state as me always. This means I can only focus on the branches below that state. To keep memory in check i also recalculate payoffs instead of storing the result for each combination of states and games. The final algorithm I ended up with works like this:

Consider the final subgames and pick a Nash equilibrium as solution.
When looking at subgames higher up the tree, I use the choices (not payoffs) computed in 1, and use those choices to play out the game. Then I compare end results to get the payoff matrix for that subgame.
As before, I iterate step 2 until I reach the root node.

This seems intuitively pretty reasonable.

Experimental results

The above method gives me a strategy that partly takes the imperfect information nature of the game into account. At many states it detected mixed strategies that had much higher payoffs compared to the pure versions. The strategies smashes all my previous best strategies by winning 1.75% more games.

The mixed strategy seems to play even more aggressively for results close to a 1000, and allowing heavy overshoot.

At this point, I was not really sure how to approach the game in a better way. In fact I was pretty ready to admin defeat for quite some time. Of course, immediately after i wrote that, I found this thesis, and this report.

Lots of new concepts to learn!

Attempting to solve Get 1000

For quite some time I have been trying to completely solve the Get 1000 game. More specifically I am trying to find the strategy in a 1 on 1 game of Get 1000 that maximises the chance to win.

Analysis of a game with one choice left. If I analyse this sub-game using expected value, I return the average of the distances to 1000. In this case 184 for strategy 1 (S1) and 107 for strategy 2 (S2). This is the wrong metric though, a better metric (if the goal is to win in a 1 on 1 game) is to count wins for each strategy. In this case 1 draw, 1 win for strategy 1 and 4 wins for strategy 2.

Solving for expected value rather then winning

My initial attempt at solving the game failed spectacularity, since I attempted to solve the game by minimising the average distance of the expected value to a 1000. This is an easy to compute strategy (using a sort of bottom up dynamic programming, where I start with the easy sub-games above, and calculate backwards to the top), but it is the wrong goal. This leads to a strategy minimising the distance to 1000 on average. This interestingly enough differs quite a lot from the goal I wanted to solve, which was to maximise the chance to win any 1 on 1 game.

The strategy that bases itself of minimising the distance to 1000 curiously has a big lump of results around a distance of 50, while the win based strategy has more games at distance of 0 and 100, as well as more games with very heavy over or undershoot.

Since Get 1000 is quite small I can calculate how much the two strategies differ by running all possible games. Above is the result of such a calculation. The two strategies draw 41.2% of the time, while the win based wins 30.8% and the distance based wins 28% of the time.

Trouble with situations where choices are equally good

After figuring out I had the wrong goal, I found a way to create a strategy based on wins rather than expected value (this is much harder to compute, even using the same bottom up approach, since it is not possible to collapse results to an average, and ever growing lists of results must be compared). These strategies I suspect are very close to optimal, but there was something funky going on.

There are situations in my calculations where two placement choices have equal amounts of winning sub-games. Initially I thought I could just set an order of preference of my choice for these, but the resulting strategies beat each other when applied to all possible games. If the order of preference did not matter this should not happen.

For the longest time I could not figure out why this happened. I started questioning whether the markov property held in the game (I am still not 100% sure it does).

Enlightenment

At this point I took a few steps back and looked at what would be the correct framework to model this game in. Turns out it can be modelled as a Markov Decision Process. That in itself was not very helpful, but it eventually got me reading about the expectiminimax algorithm. Expectiminimax is a version of minimax for games with chance involved. While I had to modify it a bit for a simultaneous turn game, I implemented it for some subproblems of get 1000, which I could calculate to the bottom.

While implementing it I realised that I again would have to code resolution for when two choices are equally good. While googling a bit about that, I randomly read about Nash Equilibrium, and mixed strategies. I was already aware of most of this, but it suddenly it dawned on me that my game might contain mixed strategies which could effect the outcome my expectiminimax calculation, and which I needed to take into account.

Wrong payoffs propagated in expectiminimax

Indeed, after searching for a bit, I found several cases where a mixed strategy is needed. The example below shows a expectiminimax situation where a mixed strategy is needed to get the best outcome.

A Get 1000 situation as solved by expectiminimax. The two games on top are the current situation for two players. To make a decision in expectiminimax we must then compute the payoff matrix by recursively analysing all possible sub-games until the end (returning expected payoffs), and then solve the payoff matrix. Using the solver here, this particular sub-game has the payoff of -98/39 (- means in favour of player 2). In this situation: Player 1 should play ones at ratio of 23/39 and hundreds 16/39, and player 2 should play tens at a ratio of 11/39 and hundreds 28/39.

While this exact situation will probably not arise assuming perfect play, the result still might matter since expectiminimax depends on all subgames propagating correct payoffs.

The road ahead

I need to include the support enumeration or theLemke-Howson algorithm for finding nash equlibrium in the placement situations that require it, and then I need to somehow make expectiminimax run for the full game. Currently I can only run expectiminimax (without Lemke-Howson) in reasonable time, for a game which has 6 placements left.

From AI: A modern approach, it seems A/B pruning can be used, but it seems to be less effective on games with chance. I guess it is worth a shot.

Gl hf to me…

Artifact 1.0.4 – Hello integer overflowing highscore!

Yesterday I finally finished some of my planned Artifact updates. The new version can be downloaded from here. Below is a detailed account of the changes in this version.

Added a game mode (rascal), where you can not lose:

As my 4 year old daughter was playing the game I had to keep typing cheat codes to keep her alive. This made me realise that I could introduce a game mode where it is not possible to lose, and where the player has infinite resources. Once I added the rascal mode she played for quite a while, and she even figured out some smart plays all by herself.

Removed global score tracking:

Global score tracking from games not played on a server will always be prone to modified clients posting fake scores. This can be mitigated though obfuscation, but not really solved. My implementation was also very bad, and very hard to maintain. Maybe I’ll revisit this one day, but for now I am glad its gone.
Removed hash checks of local data:

I do not care if you hack your local files so that you have insane scores. Hack the game all you want!
Prepare for OS X removal of some carbon audio API:

I kept getting this message in my logs:

WARNING: 140: This application, or a library it uses, is using the deprecated Carbon Component Manager for hosting Audio Units. Support for this will be removed in a future release. Also, this makes the host incompatible with version 3 audio units. Please transition to the API’s in AudioComponent.h

The solution was to upgrade openal-soft by building from source, and replace the old openal.dylib that came with Slick2D with the libopenal.dylib built, which I guess uses the API Apple wants you to use.

Artifact-1.0.2

Today I released Artifact-1.0.2 after finally getting my ass around to create a close to fully automated build script for Mac OS X (a topic for another blog post). The full changelog is listed below, but I instead recommend you go get it and try it!

Changelog:

Added full screen and resolution management in game.
Removed splash screen.
Adjusted difficulties and added new names (Apprentice, Journeyman, Master).
Added additional fire button, allowing better control using a touch-pad.
Redesigned second orb with additional graphics and new behavior.